导论
Big O notation
bounds
- f(n) is O(g(n)) if there exist constants c > 0 and n0 ≥ 0 such that 0 ≤ f(n) ≤ c · g(n) for all n ≥ n0.
- f(n) is Ω(g(n)) if there exist constants c > 0 and n0 ≥ 0 such that f(n) ≥ c · g(n) ≥ 0 for all n ≥ n0.
- f(n) is Θ(g(n)) if there exist constants c1 > 0, c2 > 0, and n0 ≥ 0 such that 0 ≤ c1 · g(n) ≤ f(n) ≤ c2 · g(n) for all n ≥ n0.
limits
If lim n→∞ f(n) / g(n) = 0 then f(n) is O(g(n))
If lim n→∞ f(n) / g(n) = ∞ then f(n) is Ω(g(n))
If lim n→∞ f(n) / g(n) = c for some constant 0 < c < ∞ then f(n) is Θ(g(n)).
Proof. for any ε > 0, there exists n0 such that c − ε ≤ f(n) / g(n) ≤ c + ε for all n ≥ n0. Choose ε = c/2 …
Stirling’s formula: $ n!$ ~ $ \sqrt{2 \pi n} (\frac{n}{e})^n $
算法策略
分治(divide and conquer)
思想:
- Breaking it into subproblems that are themselves smaller instances of the same type of problem.
- Recursively solving these subproblems.
- Appropriately combining their answers.

更快的乘法
Suppose x and y are two n-integers, and assume for convenience that n is a power of 2. (不足则补零)

2^n只要左移n次即可
递推式:T(n) = 4T(n/2) + O(n)
高斯的技巧:(a + bi)(c + di) = ac − bd + (bc + ad)i; bc + ad = (a + b)(c + d) − ac − bd 只用三次乘法。
用来计算($x_Ly_R+x_Ry_L$)之后:T(n) = 3T(n/2) + O(n)
复杂度求和:$O(n) [1 + \frac{3}{2} + … + (\frac{3}{2})^k] = O(3^{log_2{n}}) = O(n^{log_2{3}})$ , 其中k = log n
(可以把分出去的子问题想象成一棵树,每层相加)
归并排序

T(n) = 2T(n/2) + O(n), 复杂度O(nlog n)
第k小的值(k-selection)
全部排序得到结果:复杂度O(nlog n)。
分治:选择v进行快速排序,将数据分为三部分

如果每次减少一半,T(n)=T(n/2)+O(n),复杂度O(n)
如果只减少一个,T(n)=T(n−1)+O(n),O(n^2)
v is good if it lies within the 25th to 75th percentile of the array that it is chosen from.
有50%概率选到好的v,至少需要选两次(几何分布期望E(X) = 1/p)
选到好的v之后至少减少1/4长度(因为25th to 75th)
T(n) ≤ T(3n/4) + O(n) = O(n)
计算逆序数
Similarity metric: number of inversions between two rankings.
• My rank: 1, 2, . . . , n.
• Your rank: a1,a2 , . . . , an.
• Songs i and j are inverted if i < j, but ai > aj .

问题:如何combine?:排序,分别排好之后就清楚,在B中的每个元素,有多少比它大的数在A中。

T(n) = 2 · T(n/2) + Θ(n)
贪心(greedy)
局部最优以求全局最优(尽量)
最小生成树(MST)
(详见 “特殊算法” - “图的算法” )
集合覆盖(Set Cover)

例:建学校可以覆盖一定距离范围内的城镇,求最少的学校数量。
贪心算法:不断重复,选取包含未被覆盖元素的最大集合Si。
Lemma Suppose B contains n elements and that the optimal cover consists of OPT sets. Then the greedy algorithm will use at most ln n · OPT sets.
Proof.

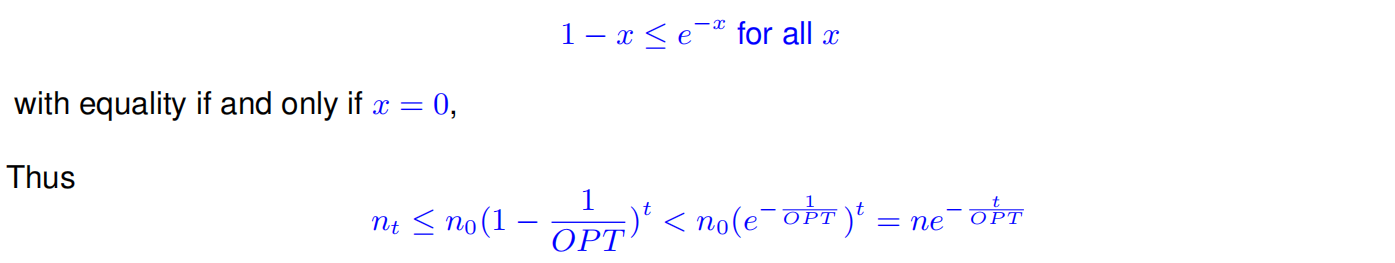
当t = ln n · OPT时,nt严格小于1,也就没有未被覆盖的元素了。
动态规划(dynamic programming)
思想:定义一组子问题,先解决最小的问题,用小问题的答案来支持大问题的求解,依次解决所有的小问题,直到解决所有的问题。
为什么不用递归?分治法:问题规模一次减小一半,DP:问题规模一次只减小一点点
需要考虑的问题:子问题是什么?边界条件(表格中最先填进去的值)?出口(最终的大问题在哪里)?
最长递增子序列(Longest Increasing Subsequences)
input: a sequence of numbers a1, . . . , an
子序列:从中挑出数字,先后顺序不变。
类比DAG的路径问题:从小数指向大数是有向边,实际就是在找形成的DAG的最长路径。

如果没有边(i, j),那就是L(j) = 1 + 0 = 1
复杂度$O(n^2)$,DAG最多n(n-1)/2条边。
编辑距离 (edit distance)
拼写检查一旦遇到一个可能拼错了的词,就要找到与它最相近的词
两个string的距离:在多大程度上相互对齐(有不同的对齐方式)

编辑距离:最小的对齐的cost(字母不同的行数)
字符串x[1, . . . , m] and y[1, . . . , n],子问题:for 1 ≤ i ≤ m and 1 ≤ j ≤ n, E(i, j): 前缀x[1, . . . , i] and y[1, . . . , j] 的编辑距离。
E(i, j) = min{1 + E(i − 1, j), 1 + E(i, j − 1), diff(i, j) + E(i − 1, j − 1)}
对应的三种情况:
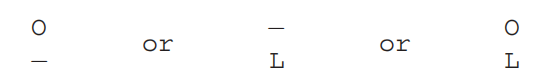
填表求解,复杂度O(mn)
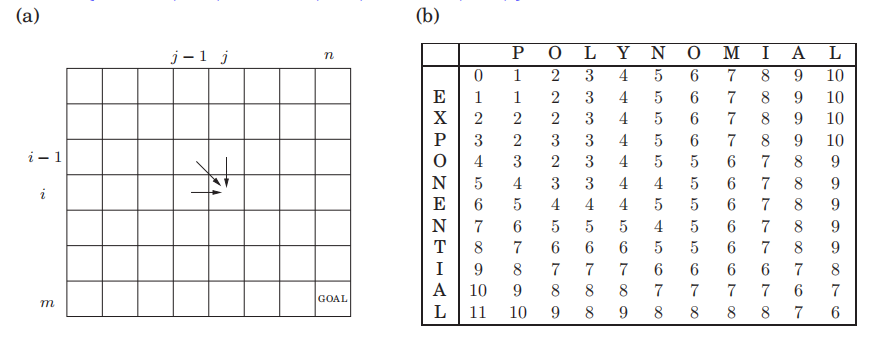
节省空间?其实只保留正在工作的两行即可。
背包问题 (knapsack)
背包容量为W,有n个物品,重量wi,价值vi,最大化价值。
类型1:无限物品 (Knapsack with Repetition)

用一维表即可,复杂度O(nW)
类型2:每样物品只有一个 (Knapsack without Repetition)

| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | ||||||
| {1} | ||||||
| {1,2} | use this | or this | ||||
| {1,2,3} | to decide this | |||||
| {1,2,3,4} |
最长相同子序列(Longest Common Subsequence)
与编辑距离相比,求最短变成求最长
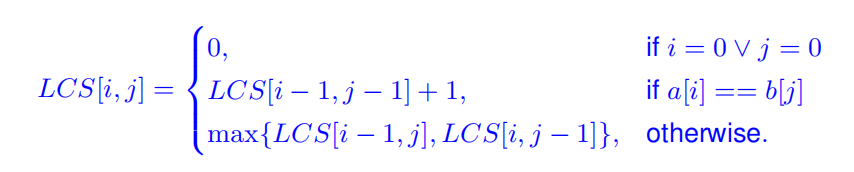
如果是最长相同子串(中间不能断开)呢?otherwise(i,j不相同)这一项直接为0。
链式矩阵相乘

分析:相乘顺序可以表示成二叉树:
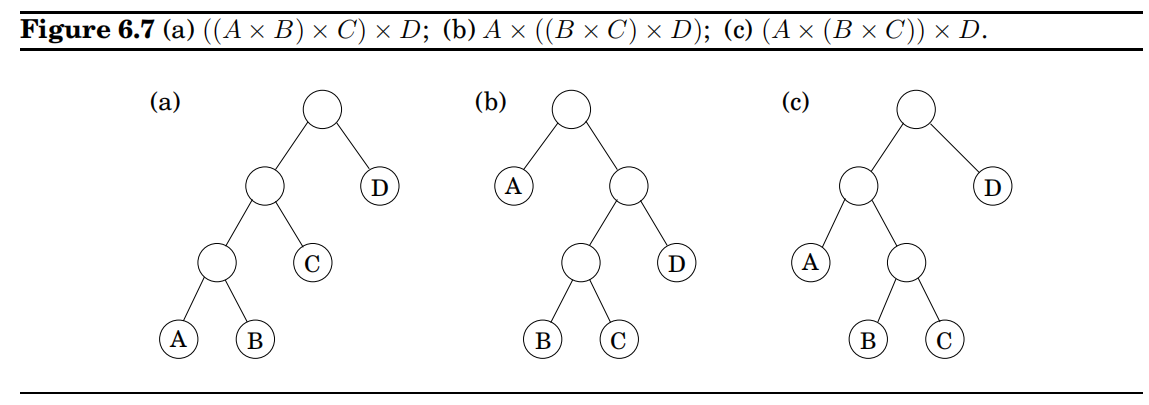
如果一个树是最优的,那么它的子树也是最优的。
子树对应的子问题:

构造二维表格,每个格计算时间O(n),总共用时$O(n^3)$
更复杂的最短路径问题
最短可靠路径
图G从s到t最短路径,但是最多用k条边。
子问题:dist(v,i) 从s到t使用i条边的最短路径
所有顶点间的最短路径
使用Bellman-Ford算法|V|次,$O(V^2 E)$
接下来介绍Floyd-Warshall算法:$O(V^3)$
思想:u和v之间的最短路径通常要用到一些“中间节点”,可以一开始不允许使用任何中间节点,然后逐渐扩展可用的中间节点的集合。每增加一个新的中间节点,就更新所有的最短路径。如果第k轮的时候,u到v之间出现新的最短路径,那这个新的最短路径一定是经过第k个点的,否则在k轮之前这个路径就应该被发现。

节点k不是在第k轮才加入的吗?怎么dist(i,k,k-1)在之前就被求出来了?答:0 ~k-1是可用的中间节点的范围,两端节点还是可以在0 ~ k-1范围以外的。每次更新,i和j的范围都是从0到n。
旅行商问题(TSP)
图上节点1~n是城市,旅行商人从1出发,把每个城市都恰好经过一遍,最后回到1,路径要最短。(任意两个城市之间的距离已知)

$2^nn$个子问题,每个子问题为O(n)。总共$O(2^nn^2)$【说明DP并不都能降到多项式时间】
树中的独立集
A subset of nodes S ⊆ V is an independent set of graph G = (V, E) if there are no edges between them.
找最大独立集比较难,但是如果是在树上就可以利用DP。
自底向上求解整棵树。对于节点u,如果独立集包含u,那么必不能包含其儿子(否则有边相连),但是可以包含其孙子。如果独立集不含u则可能包含其儿子。

线性规划(linear programming)
求解优化任务,任务的特点是约束条件和优化准则都可以表示为线性函数。
给定一个变量集合,使其满足一组线性方程or不等式,使目标线性函数值最大or最小。
利润问题

LP Formulation以及可行域:



没有最优解:不可行或者无界。
求解:使用单纯形法。
有时候解决实际问题要求解是整数,可能要四舍五入,仍有一定差距。于是有整数线性规划问题,它没有多项式时间算法。
LP的标准型
标准型:所有的变量非负,采用等式约束条件,都以目标函数最小化为目标
求最大值变最小值:乘-1即可。
等式约束条件:松弛变量s:x ≤ 200 → x + s = 200, s ≥ 0
所有变量非负:对不确定符号的x,引入两个非负变量$x^+, x^-$,用$x^+ - x^-$代替x。
对偶(duality)
还是上面的利润问题:

我们希望不等式左边能凑出objective function x1 + 6x2,然后希望右边尽可能小:
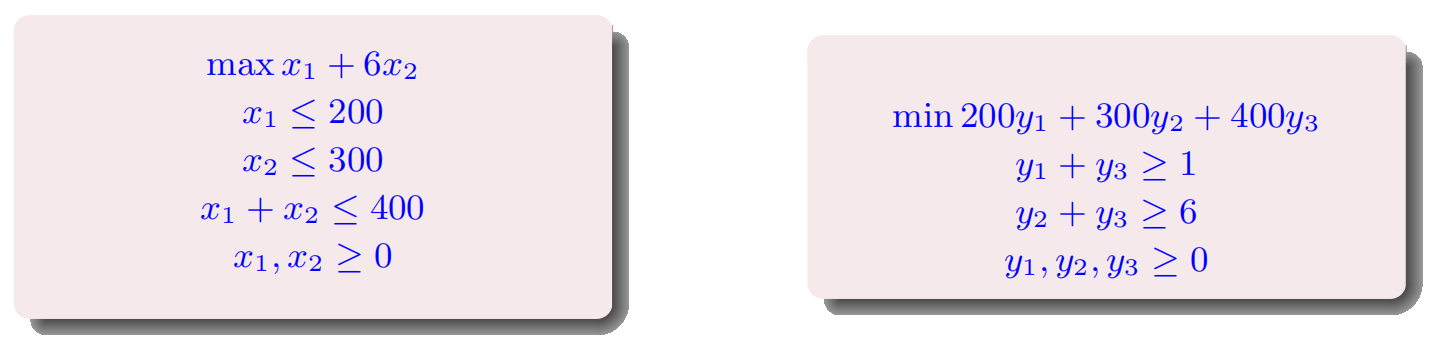

Theorem (Duality) If a linear program has a bounded optimum, then so does its dual, and the two optimum values coincide(一致).
互补松弛条件 (Complementary Slackness):如果一个变量在原始问题中的最优解中为非零,则对应的对偶问题中的约束条件的松弛变量为零,反之亦然。

binding: 不等号取等号
最短路径的LP形式

集合覆盖(Set Cover)的LP形式


$x_s$表示集合s是否被选中。第一个不等式表示e至少要在选出来的一个s中。
例:U={e1,e2,e3,e4,e5},s1={e1,e2,e3},s2={es,e4,e5},s3={e1,e5}
则对于e1来说,$x_{s_1}+x_{s_3}≥ 1$,也就是s1和s3至少有一个要被选中,才能覆盖到e1。
如果要求每个元素至少被覆盖r次,第一个不等式≥r即可。
单纯形法 (simplex method)
对于约束不等式的一个子集,如果有唯一的点满足对应的所有等式,且该点是可行的,那就是一个顶点。
let v be any vertex of the feasible region, while there is a neighbor v ’ of v with better objective value: set v = v ’ (从一个顶点开始,不断寻找更优的邻居直至没有更优的邻居)
如果解空间是N维的,如何定义邻居?:N个平面(不等式)确定一个顶点,N个不等式中有N-1个相同就是邻居。有些顶点可能有大于N个平面,因为实际是多个顶点合在一起(如果多个顶点合在一起,应该采用退化,为bi引入某个随机的微小改变)。

现在假如LP问题是一般形式的最大值问题。
Task 1 in the Origin The origin is optimal if and only if all ci ≤ 0.
Task 2 in the Origin We release the tight constraint xi ≥ 0 and increase xi until some other inequality, previously loose, now becomes tight. We have exactly n tight inequalities, so we are at a new vertex.
以上task在原点上很容易,如果不在原点(origin)则可以坐标变换移动到原点:
如果定义u的n个不等式中的一个为ai · x ≤ bi,那么对应的yi = bi − ai · x。根据这些将x表示为y的函数,代回到原问题。于是得到修改后的LP问题,在这个问题中yi ≥ 0, 并且u是这个y-空间的原点。
example:
- 首先x1= x2 = 0,放松x2使其增加,它会首先触碰到红色不等式的边界范围。将y1 = x1, y2 = 3 + x1- x2代入得到右边的新形式。

- 现在还可以增大y1(y2在目标函数中系数已经为负),于是重复1,右边的形式所有ci都为负,此时原点处就是optimal

但是单纯形法之所以可以从原点开始,是因为不等式右侧都是正数,如果不是该如何寻找起始顶点?好在寻找起始顶点的问题也可以被规约为LP并求解。


example:


LP如果是无界的:在探索邻居时会发现新的线性方程组有无穷多的解。
特殊算法
数字的算法
进制不同不影响复杂度(换底公式),数字N的size就是O(log N)
各种操作的复杂度
n bits, n = log N
- addition: $O(n)$ 【最多进一位】
- multiplication: $O(n^2)$ 【相当于(n - 1)个加法】
- times 2: $O(1)$【左移1位】
- division (modular): $O(n^2)$
- Modular add: $O(n)$ 【结果大于N则减N】
- M mul: $O(n^2)$【结果除以N】
- M exp: $O(n^3)$ 【最多n次循环调用(每次将指数除以2),每次一个乘法】
- M gcd: $O(n^3)$【Euclid算法,2n次循环调用,每次一个mod】
- M inv: $O(n^3)$【扩展Euclid算法】
- M div: $O(n^3)$【$b/a\mod N = b a^{-1}$】
乘法的算法
Multiplication by Al Khwarizmi

正确性?—— 左边是偶数,相当于下图算式中全是0的这一行


模的规则
x = qN + r with 0 ≤ r < N, r = x modulo N
x ≡ y mod N ⇔ (x − y) = cN
b除以a,商为整数,且余数为零, 我们就说“a整除b”或“b能被a整除”,即a|b
rules

模的指数运算: x^y mod N
如果只是每次乘x,对于500位的y来说至少要乘2^500次,太多了。


最大公因数(Greatest Common Divisor):gcd(x, y)
Euclid’s rule: If x and y are positive integers with x ≥ y, then gcd(x, y) = gcd(x ( mod y), y).
Proof. gcd(x, y) = gcd(x − y, y),重复减即可
| |
Lemma If a ≥ b ≥ 0, then a mod b < a/2
Proof.
- if b ≤ a/2, a mod b < b ≤ a/2;
- if b > a/2, a mod b = a − b < a/2
这意味着在任何连续的两轮之后,两个参数x y的值至少减半,也就是每个的长度至少减少1位。2n次循环调用。
An Extension of Euclid’s Algorithm
Lemma If d divides both x and y , and d = ax + by for some integers a and b , then necessarily d = gcd(x, y)
Proof. 显然d ≤ gcd(x, y)。gcd(x, y) 能整除 x and y, 一定也能整除 ax + by = d. 则d ≥ gcd(x, y)
证明d = gcd(a, b),即找到两个x y使d = ax + by(a b 必一正一负)
模倒数
We say x is the multiplicative inverse(乘法逆元) of a mod N, if ax ≡ 1 mod N
至多有一个这样的x,记为$a^{-1}$。逆元不一定存在。
Lemma If gcd(a, N) > 1(a n不互素), then ax /≡ 1 mod N(逆元不存在).
Proof.
ax mod N = ax + kN, gcd(a, N) 整除 ax mod N。所以当gcd(a, N) > 1时,将有ax /≡ 1 mod N。
If gcd(a, N) = 1, then extended Euclid algorithm gives us integers x and y such that ax + Ny = 1, which means ax ≡ 1 mod N.
求a mod N的逆元:看 gcd(a, N) = 1,找ax + Ny = 1, 于是ax ≡ 1 mod N
素数与素性测试
费马小定理:If p is a prime, then for every 1 ≤ a < p, a^{p −1} ≡ 1 (mod p)

permute(重新排列):i不同,a \ i mod p将各不相同且非零。否则a i = a j mod p 即 i = j mod p。
费马小定理并非充要条件。只能希望对于合数N,大部分a无法通过测试。
Carmichael Number:对所有与N互素的a都能通过测试。比较罕见。
Non-Carmichael Number:只要有一个a不通过测试,那么至少有一半的a < N都通不过测试。

以下算法假阳性的概率小于$1/2^k$

素数的随机生成:

x个数里有x/ln(x)个素数,则n位数是素数的概率为 1/log x = 1/n。
每次挑选一个数验证是否素数,每次有1/n可能停下,平均需要O(n)轮次。M exp复杂度 $O(n^3)$ ,整体就是 $O(n^4)$。
图的算法
图的DFS与连通性

被explore到的是“树边”,否则是“回边”(图中虚线)
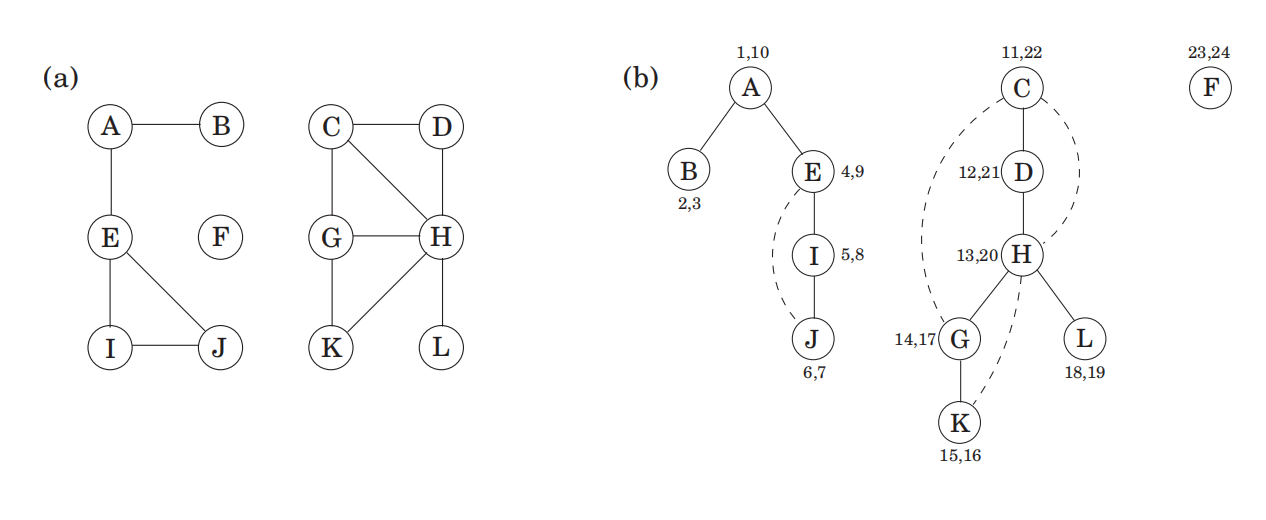
An undirected graph is connected, if there is a path between any pair of vertices.
A connected component is a subgraph that is internally connected but has no edges to the remaining vertices.
DFS外部循环的explore过程每从一个顶点开始,就能确定一个包含该顶点的连通部件。可以划分出连通部件
引入计时机制(在上图也有体现)。

For any nodes u and v , the two intervals [pre(u), post(u)] and [pre(v), post(v)] are either disjoint(分离) or one is contained within the other(一个包含另一个)。原因:实际就是顶点在堆栈中的时间段,先进后出。
与无向图不同,有向图除了树边,还分前向边、回边和横跨边。
- Tree edges are actually part of the DFS forest.
- Forward edges lead from a node to a nonchild descendant(后裔) in the DFS tree. (当然是nonchild,如果是child的话那就是树边)
- Back edges lead to an ancestor(祖先) in the DFS tree.
- Cross edges lead to neither descendant nor ancestor.(就是从一个顶点指向已经被完全访问过、进行过postvisit的顶点的边)


(上面右图的 [ 和 ] 分别代表previsit和postvisit)
DAG:有向无环图
A cycle in a directed graph is a circular path v0 → v1 → v2 → . . . vk → v0
Lemma. A directed graph has a cycle if and only if its depth-first search reveals(探测到) a back edge.
Proof.
- 充分性:(u,v)是回边,则存在包含该边以及从v到u路径的环
- 必要性:如果含有环 v0 → v1 → v2 → . . . vk → v0,假设最先被访问的点为vi,环上其他顶点均为vi在搜索树中的后裔。边v_{i-1}→vi即为回边。
DAG没有回边。
Lemma. In a DAG, every edge leads to a vertex with a lower post number.
DAG可以被拓扑排序,即可以通过顶点的post值降序进行线性化。
Lemma. Every DAG has at least one source and at least one sink.
源点:post值最大,入度为0。汇点反之。
强连通部件
Two nodes u and v of a directed graph are connected if there is a path from u to v and a path from v to u.
This relation partitions V into disjoint sets(分离的集) that we call strongly connected components (SCC).
Lemma Every directed graph is a DAG of its SCC.
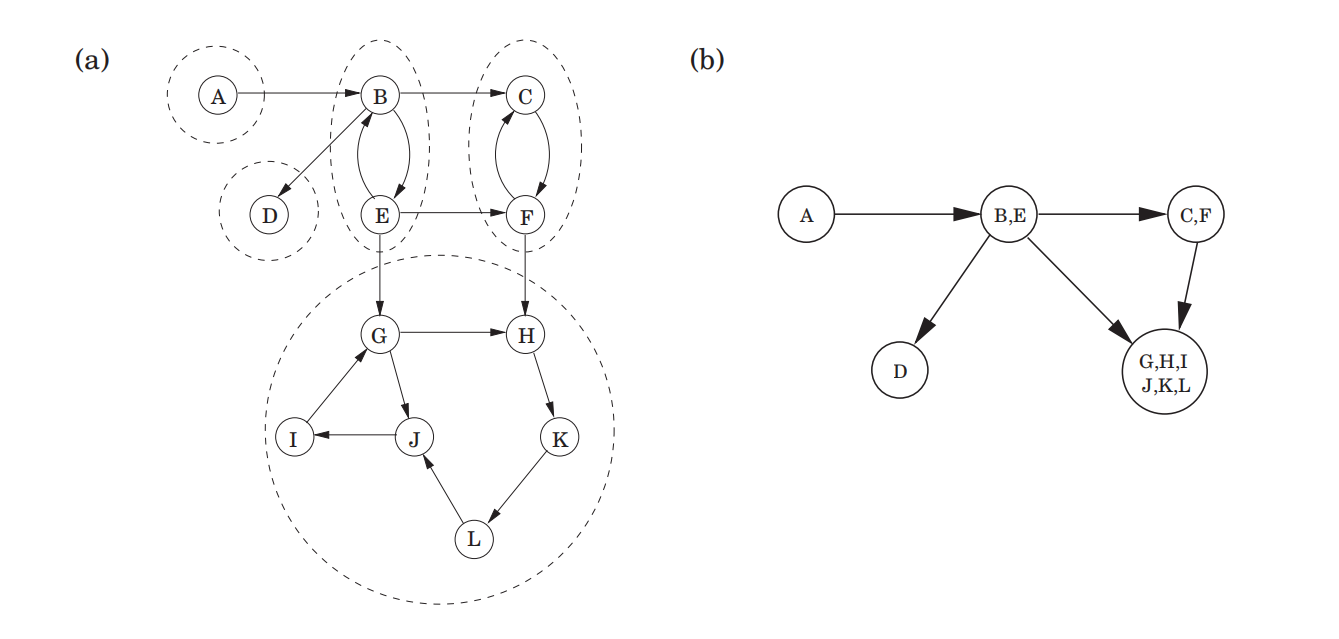
Lemma If the EXPLORE subroutine start at node u, then it will terminate precisely when all nodes reachable from u have been visited.
意味着如果在汇点强连通部件中的某个顶点调用explore,将恰好得到这个SCC。
Lemma If the EXPLORE subroutine at node u, then it will terminate precisely when all nodes reachable from u have been visited.
Lemma If C and C ′ are SCC, and there is an edge from a node in C to a node in C ′ , then the highest post number in C is bigger than the highest post number in C ′ .
那么这些SCC也能根据它们各自的最小post num进行线性化的排序。
图G的反转图$G^R $,在G上的sink在$G^R$上是source。
综上,输出所有SCC的办法:
- 在$G^R$上DFS,找到post值最大的顶点u
- 在G上对u进行DFS,得到一个汇点SCC,将其删除
最短路径
The distance between two nodes is the length of the shortest path between them.
每条边没有权值,求从一个点出发求它到剩下所有点的距离:使用BFS(第1批被访问的是距离为1,以此类推)
有边长or权值:Dijkstra算法(高级数据结构笔记讲过,不赘述)
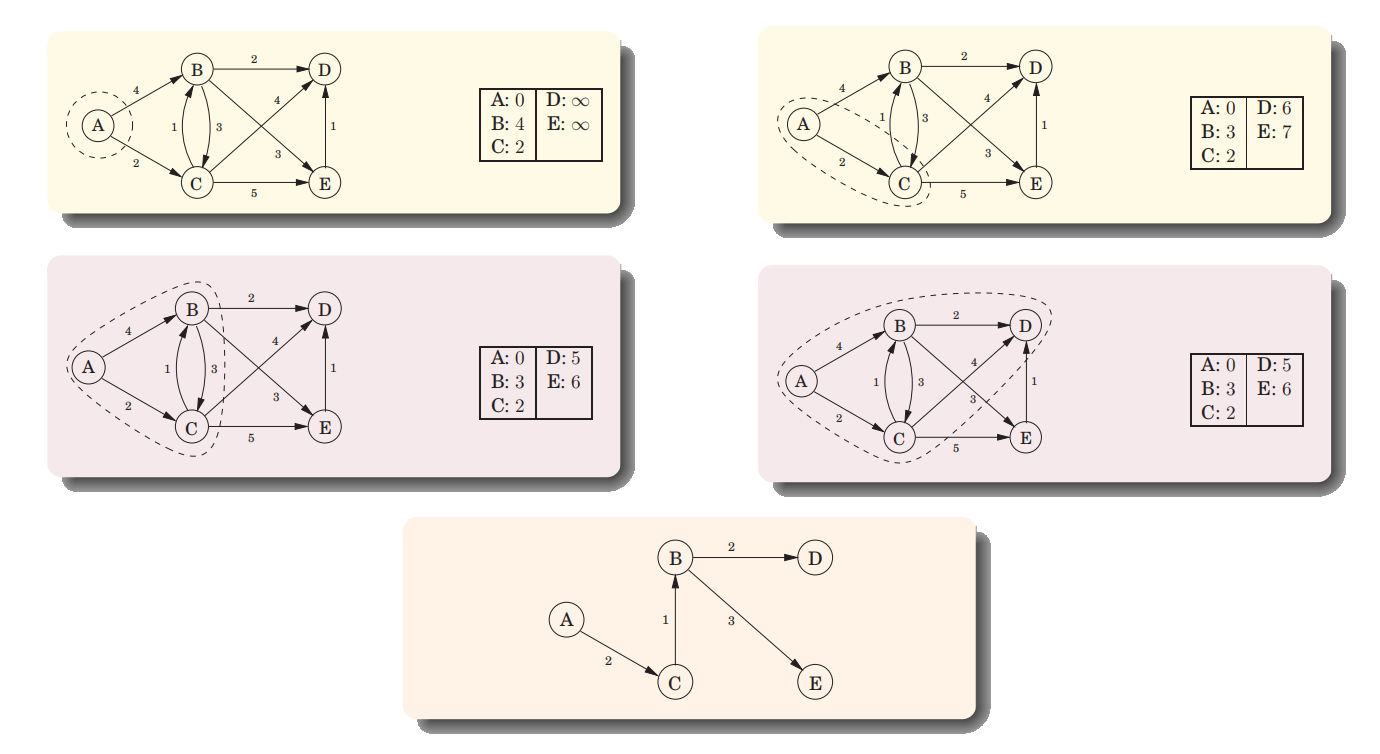
最短路径的局部也是最短路径
正确性证明:S is the set of vertex with the dist being set. 证每次向S中添加点时都有x.d == dist[x],x.d表示s到x的真实的最短距离,dist[d]表示x在dist数组中的对应值。
Proof. 对源点肯定成立。假设第k次加入的结点仍为最短路径,第k+1次加入u。设u为第一个不满足x.d == dist[x]的点,设u的最短路径为s-> … -> y -> … -> u,y为该路径上不在S中的第一个点。dist[y] = y.d ≤ u.d<dist[u],而u加入时有dist[u] ≤ dist[y],矛盾。
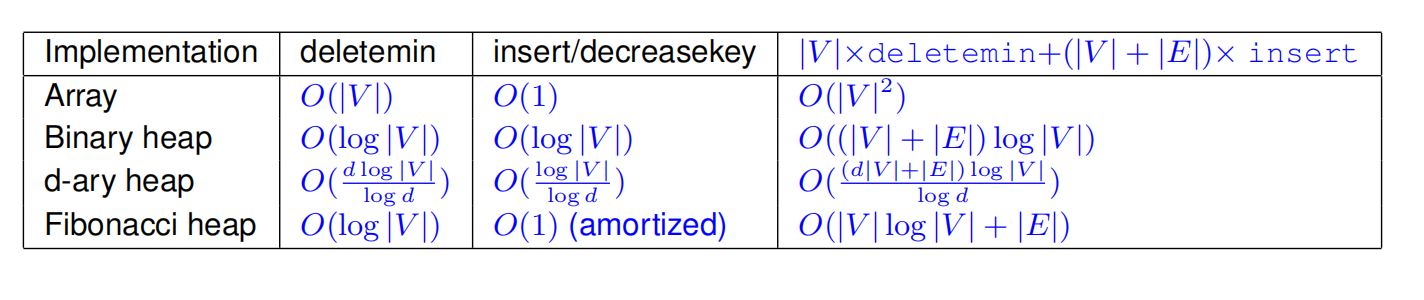
算法复杂度:|V| deletemin and |V | + |E| insert/decreasekey operations,具体视优先队列的实现而定。
Dijkstra算法中边的权值不能为负:不会因为负边的出现而更新已经计算过(收录过)的顶点的路径长度,可能有某些顶点最终计算出的路径长度不是最短的长度。
Bellman-Ford Algorithm
| |

最短路径最多有 |V| − 1 条边,所以更新 |V| − 1次即可。
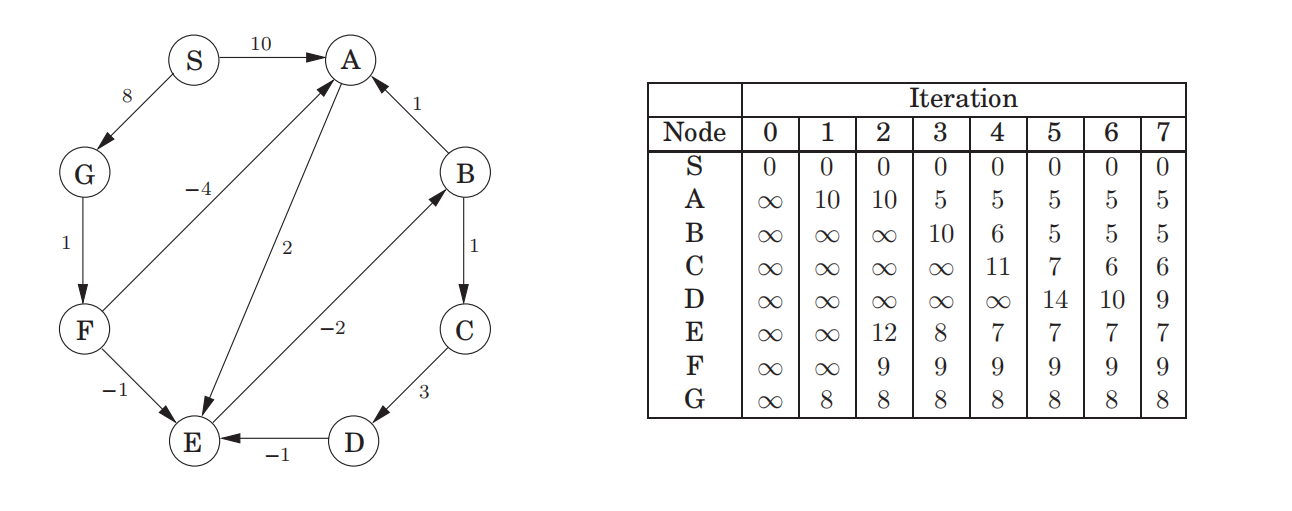
如果有负环也不行。可以在|V| − 1次次更新之后再更新一次,检查是否不变了。
DAG天生没有负环,按照拓扑排序的顺序进行update。


不难发现这其中蕴含着动态规划的思想:$dist(v) = \min_{(u,v)∈E} {{dist(u) + l(u, v)}}$
Even can find longest paths in a DAG by the same algorithm: just negate all edge lengths.
最小生成树(MST)

Lemma (1) Removing a cycle edge cannot disconnect a graph.
Lemma (2) A tree on n nodes has n − 1 edges
Proof. 从一个空图开始,一次构建一个边。每个节点都与其他节点不连接,各自是一个连通部件。当添加边时,这些组件合并。由于每条边都结合了两个不同的组件,所以当树完全形成时,恰好增加了n - 1条边。当一条特定的边(u, v)出现时,我们可以确定u和v位于独立的连接分量中,否则它们之间就已经存在一条路径,这条边就会创建出一个环。
Lemma (3) Any connected, undirected graph G = (V, E) with |E| = |V| − 1 is a tree.
Proof. 它是(2)的逆命题,我们只需要证明G是无环的。当图包含一个环时,从这个环中删除一条边,直到得到无环的图G‘,G’ = (V, E‘), 由(1),G’也是连通的。因此G‘是一棵树。根据(2),|E’| = |V| − 1,所以E’ = E,实际没有边被移除,G一开始就是无环的。
Lemma (4) An undirected graph is a tree if and only if there is a unique path between any pair of nodes.
Proof. 如果多于1条则有环。
利用贪心的思想解决MST:
Kruskal’s MST algorithm starts with the empty graph and then selects edges from E according to the following rule: Repeatedly add the next lightest edge that doesn’t produce a cycle.
其正确性来自于分割性质:
Lemma Suppose edges X are part of a MST of G = (V, E). Pick any subset of nodes S for which X does not cross between S and V \S, and let e be the lightest edge across this partition. Then X ∪ {e} is part of some MST.
Proof. (懒得翻译了)
Edges X are part of some MST T; if the new edge e also happens to be part of T, then there is nothing to prove.
So assume e is not in T. We will construct a different MST T ’ containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T. Since T is connected, it already has a path between the endpoints of e, so adding e creates a cycle.
This cycle must also have some other edge e’ across the cut (S, V \S). If we now remove e, T ’ = T ∪ {e}\ {e’}, which we will show to be a tree.
T ’ is connected by Lemma (1), since e ’ is a cycle edge. And it has the same number of edges as T ; so by Lemma (2) and Lemma (3), it is also a tree.
Since weight(T ’ ) = weight(T) + w(e) − w(e’ ). Both e and e’ cross between S and V \ S, and e is the lightest edge of this type. Therefore w(e) ≤ w(e’ ), and weight(T ‘) ≤ weight(T)
Since T is an MST, it must be the case that weight(T’) = weight(T) and that T ’ is also an MST.
分割性质表明,任何遵循以下模式的算法都是有效的:

Prim算法中,X总是构成一个子树。每一步迭代,这个子树会生长一条边,即选择S中的顶点与S外的顶点之间的最轻边加入X。
网络流的算法
最大流问题
输油网络,每个管道有最大容量,输送过程中油无法被储存。目标是从源点到汇点输送尽可能多的石油。


转化为LP问题。
另一种形式:s到t之间增加一条容量为∞的边,最大化这条边的flow

对这个LP采用单纯形法,实际就是不断选择从s到t的一条可能路径,然后尽可能增大它的流量。
允许两条路径的flow相互抵消(相减),也就是可以撤销路径上的某些流。

(第二种情况下最多增加流量为f,最多就是撤销路径上的全部流)
剩余网络的定义:

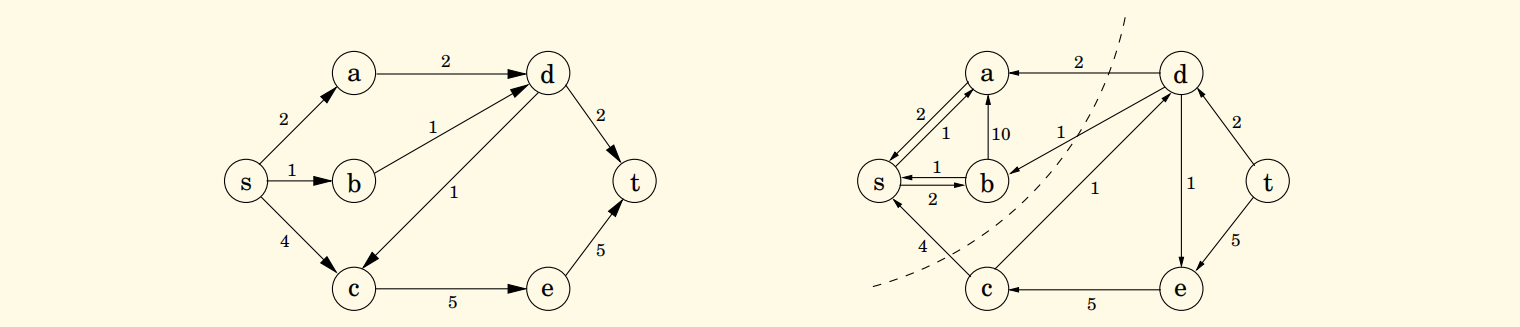
example(左边为当前的流,右边为剩余网络,粗线为选择的路径):
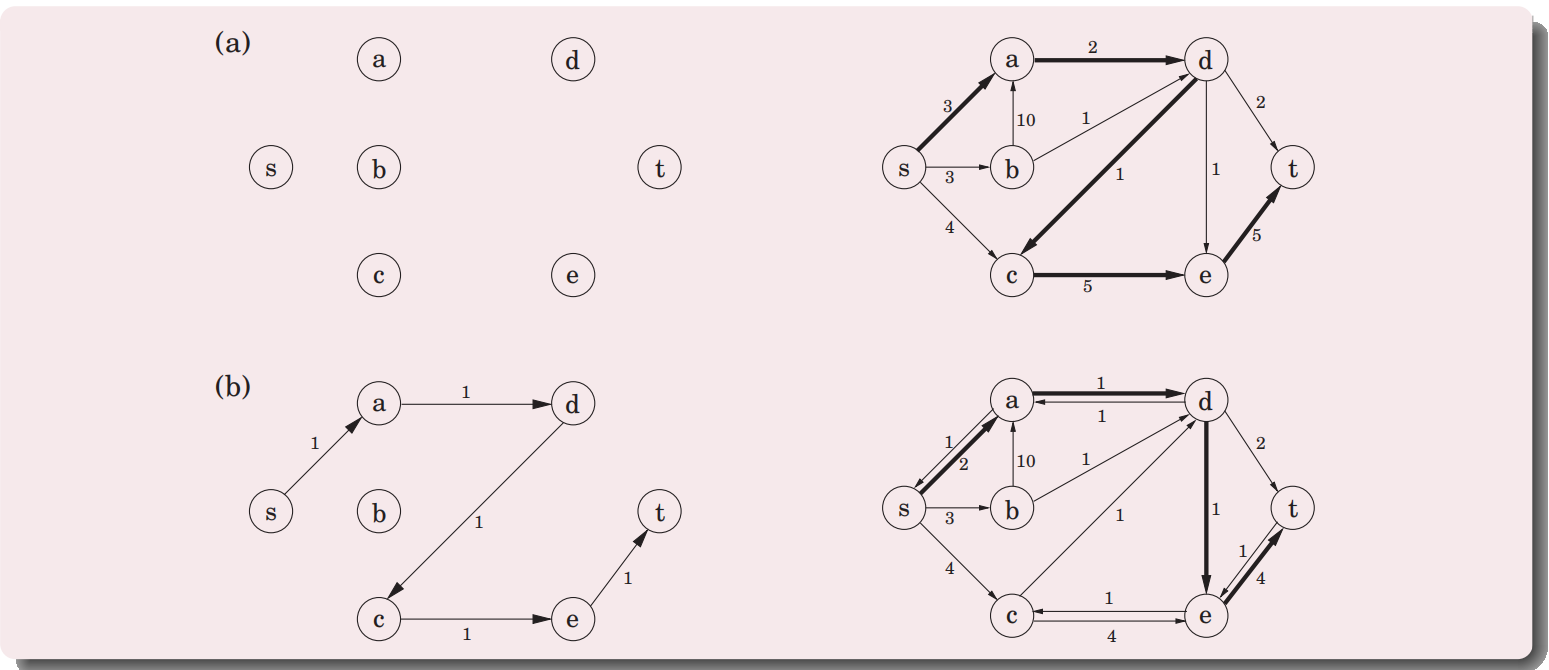
(直到最后没有s到t的路径为止)
如何证明这个流是最优的?:从流到割
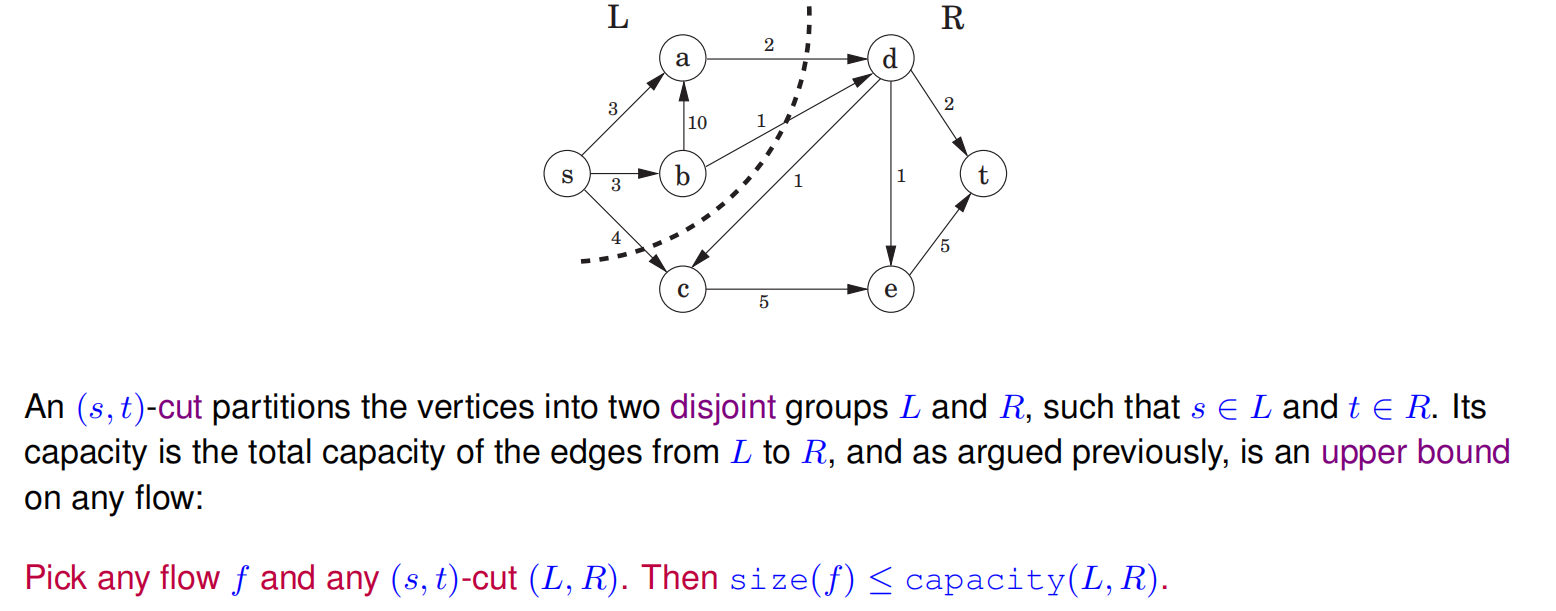
Theorem (Max-flow min-cut) The size of the maximum flow in a network equals the capacity of the smallest (s, t)-cut.
Proof.
Suppose f is the final flow when the algorithm terminates.
We know that node t is no longer reachable from s in the residual network $G^f$.
Let L be the nodes that are reachable from s in $G^f$ , and let R = V \ L be the rest of the nodes.
We claim that size(f) = capacity(L, R).
To see this, observe that by the way L is defined, any edge going from L to R must be at full capacity (in the current flow f), and any edge from R to L must have zero flow.
Therefore the net flow across (L, R) is exactly the capacity of the cut.
LP的对偶的解释:

剩余网络中,源点s可达的pi都为1,s不可达(t可达)的pi都为0。如果dij = 0代表pi = pj。
算法复杂度:寻找路径的时间是O(E)。但是迭代次数是CE,C是所有容量的上限,因为可能经常出现两个流相互抵消的情况!
如果采用BFS,寻找到最少边的路径,那么迭代次数就是VE。总用时$O(VE^2)$
如果在每个节点上都有可能消耗/产出石油?构造一个S和T,所有的产出都与S相连,所有的消耗都与T相连。最后检查是否每个点都满足输入 - 输出=消耗/产出
二部图的匹配
男孩和女孩有边相连表示彼此喜欢,找到一个配对使得配对双方都互相喜欢。

转换为最大流问题,每条边容量为1,存在完美匹配的条件是存在一个规模与最终配对数相等的最大流。
NP问题
搜索问题
- 判定问题. Does there exist an assignment to satisfy the formula in CNF? 回答yes or no
- 优化问题. given an instance of TSP, find the minimum cost tour.
- 搜索问题. Find an assignment to satisfy the formula.
A search problem is specified by an algorithm C that takes two inputs, an instance I and a proposed solution S, and runs in time polynomial in |I|. We say S is a solution to I if and only if C(I, S) = true.
S必须足够简明且在多项式时间内可验证。
三类问题互相转化不改变复杂度。
然而,有些问题目前最快算法都还是指数时间的,和穷举相比没有本质改善。
搜索问题的例子:
可满足性问题(SAT):给定一个采取合取范式的布尔公式,为其找到一个可满足的赋值或者判定该赋值不存在。
每个子句都是多个文字的析取,可满足赋值:每个子句都取值为true。
2-SAT是多项式时间可解的:如果实例I有n个变量和m个子句,构造图,2n个节点(变量及其否定),2m条边,对于每个子句A or B,加入从not A到B的边和从not B到A的边。如果图中有强连通分量同时包含x和x的否定,则I不可满足。
3-SAT及以上则是指数时间才能求解的。
TSP问题(但是限定了最高预算b):限定预算是为了方便检验解,指数时间。
Euler Path:Given a graph, find a path that contains each edge exactly once.
只要图是连通的并且除了起点终点之外所有点的度数为偶数即可,多项式时间!
Rudrata Cycle:Given a graph, find a cycle that visits each vertex exactly once.
与TSP类似,指数时间。
Minimum Cut:given a graph and a budget b, find a cut with at most b edges.
令每条边容量为1,求一个确定节点与其他所有节点的最大流,最小的流对应最小分割。多项式时间。
Balanced Cut(平衡分割):Given a graph with n vertices and a budget b, partition the vertices into two sets S and T such that |S|, |T| ≥ n/3 and such that there are at most b edges between S and T. 指数时间。
3D Matching:There are n boys, n girls, and n pets. The compatibilities are specified by a set of triples, each containing a boy, a girl, and a pet. 与二部图匹配相似,但是指数时间。
Independent Set:Given a graph and an integer g, find g vertices, no two of which have an edge between them. 指数时间。
Vertex Cover(顶点覆盖):Given a graph and an integer b, find b vertices cover (touch) every edge. 不存在多项式时间的精确算法(但是可以像集合覆盖一样,贪心算法近似)
顶点覆盖是集合覆盖的特例:对每个顶点i定义子集Si,使Si包含与i相连的所有边。要覆盖的集合就是边集E。
Cligue(团问题): Given a graph and an integer g, find g vertices such that all possible edges between them are present(即这些顶点之间两两都存在相同的边).
最长路径问题:只能枚举解决
背包问题:Seek a set of items whose total weight is at most W and whose total value is at least g. O(nW),由于是W而不是logW,因此也是指数时间。除非在一进制(unary)下,数字大小和数位大小是一样的。
subset sum(子集和): Find a subset of a given set of integers that adds up to exactly W. 指数时间。
图同构问题
NP, co-NP, NPC及其他
P, NP

NP:任何可能解的正确性都能在多项式时间内检验。
P:能在多项式时间内求解。
NP包含P,但一般认为P≠NP。
co-P, co-NP
问题A回答yes,它的补问题回答no。
A class of problems C is closed under complementation(在补问题下封闭) if for any problem in C, its complement is also in C.
P is closed under complementation. P = co-P
NP is not closed under complementation! 验证回答yes,原问题回答yes,验证回答no不代表原问题回答no!NP ≠ co-NP
NPC
A NP problem is NP-complete if all other NP problems reduce to it.
If even one NP-complete problem is in P, then P = NP.
其他
co-NPC:

NPI:属于NP但是不属于P和NPC。图同构、因数分解、判断质数可能都是这类问题。

规约(reduction)

规约的用途:
- solve. 从未知问题归约到已知问题
- proof. 从已知问题归约到未知问题。A→B,如果A很难(没有多项式时间算法),那么B也很难。
证明B是NPC问题:首先说明B是NP问题,然后将一个NPC问题A归约到B。
以下这些问题都是NPC问题。

Rudrata Path → Rudrata Cycle
Rudrata Path:求一条从s到t的恰好经过每个顶点一次的路径。


3SAT → Independent Set
子句构成三角形,相反的文字之间添加边

SAT → 3SAT
a1~ak至少有一个为真,否则y1必须为真,进而y2为真,y3为真…直至最后一个子句不满足。

如果我要求3SAT中所有变量出现不超过三次?x出现k次就分裂为x1~xk。

这样以来x1~xk必须同时为true,就相当于一个变量x。
Independent Set → Vertex Cover
S是G的顶点覆盖 当且仅当 V-S是G的一个独立集。
(如果V-S不是独立集,那么V-S顶点有边相连,那么S并没有覆盖完所有的边)
找大小为g的独立集 等价于 找大小为|V|- g的顶点覆盖。
Independent Set → Cligue
G的补集$\overline{G} = (V, \overline{E})$,其中$ \overline{E}$是所有不属于E的无序结点对。
G中的独立集就是G补集中的团。
Rudrata Cycle → TSP
如果城市u,v之间有边,则距离为1,否则距离为1+a,a≥1。TSP的预算等于节点数V即可。
为什么需要设置一个a?因为TSP对任意两个城市都有距离,但是现在的图上不一定任意两点之间都有边。
近似算法
为了多项式时间处理NPC需要的代价:

近似算法:牺牲准确性。
在优化问题中,对于实例I,OPT(I)即最优解,A(I)为算法A得到的解。算法A的逼近比例为:

逼近比例体现了最坏情况下结果偏离最优解的程度。
例如set cover的逼近比例就是ln n。
问题在于,不知道OPT是多少,如何知道逼近比例?
vertex cover
匹配:没有共同端点的边组成的集合。
没有更多的边可以加入时,达到极大匹配。

极大匹配M有M条边,2M个顶点,但是M ≤ OPT(因为匹配中的每条边必然有一个端点属于某个顶点覆盖)
逼近比例为2
聚类(Clustering)

通俗来说,就是用k个大小相等的圆将空间中这n个点完全覆盖,这些圆的最小直径是多少。
贪心算法:选择k个中心点,每次选择的下一个中心点离现有的中心点最远。
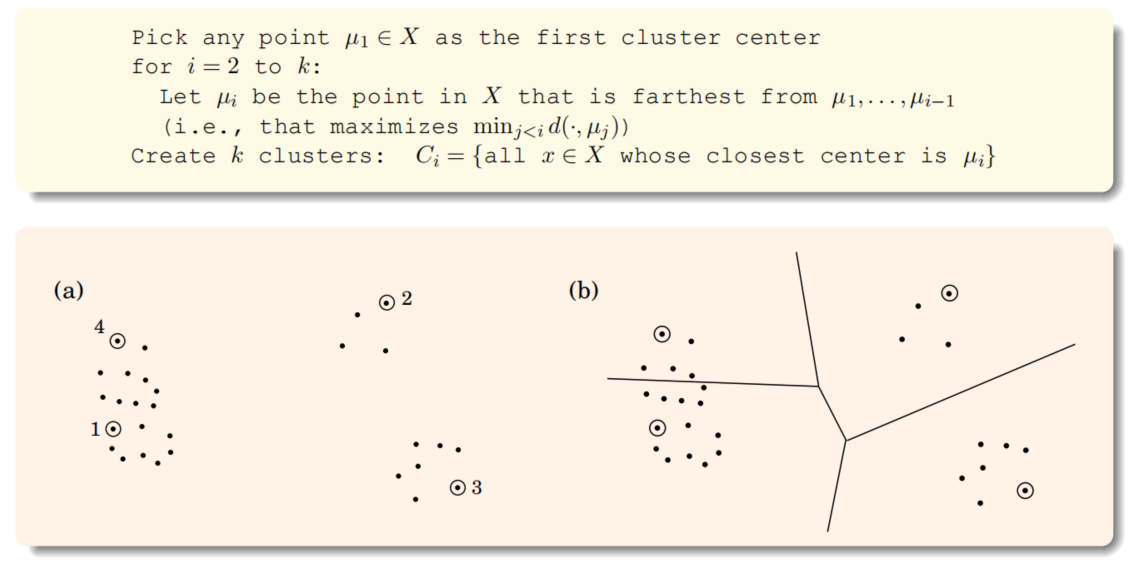
三角不等式也就是三角形的性质:d(x, y) ≤ d(x, z) + d(z, y)
解释1:如下图

解释2:

(k+1个中心点放入k个聚类,至少有两个中心点被放到同一个聚类。又知道中心点互相之间距离至少为r,那么OPT直径至少为r)
TSP(但是在几何意义上成立的)
之前TSP城市距离是随便定的,但是现在要求任意三个城市距离符合三角不等式(在几何上,真的能构成一个三角形)
TSP的环路删掉一条边就变成路径:TSP cost ≥ cost of this path ≥ MST cost
现在要从MST中构建一条商人旅行路线:
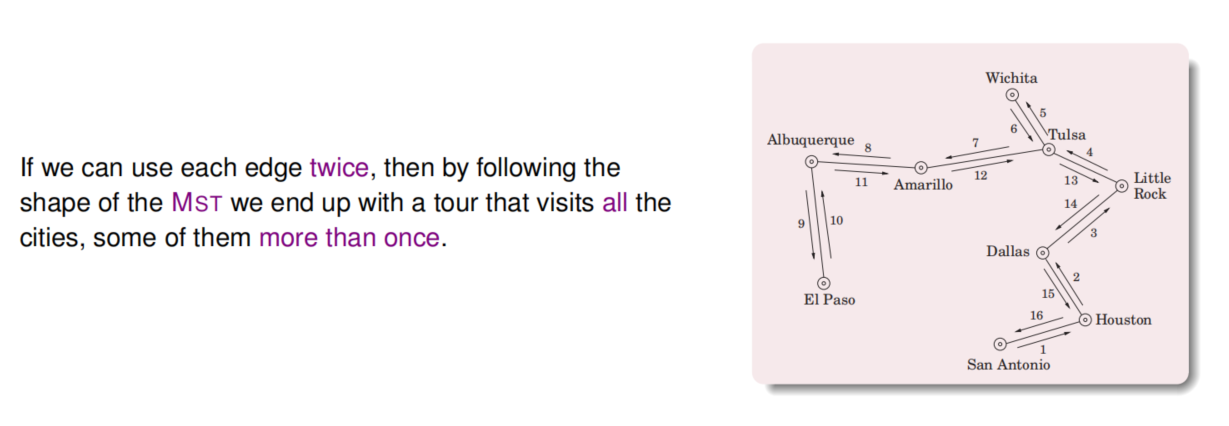
存在的问题是有些城市被访问不止一次,在“走投无路”时直接跳到某一个没访问过的城市即可,就不按照原来的MST走了。

现在OPT cost ≥ MST cost,然后算法TSP cost ≤ 2 MST cost,因此逼近比例为2。
有没有更好的算法?找到所有奇数度的点(肯定总共有偶数个),找到这些点的最小Matching加入到MST中,比double MST要好。
背包问题
要么O(nW),要么O(nV),V是物品价值的总和。W和V可能都很大。
如果把绝对价值转变为相对价值(有一点损失):


以下推导中有四样东西:没有收缩(shrunken)的最优值总和(K),收缩之后的最优值总和(第一个式子最左边),没有收缩的算法结果的值总和(第二个式子最左边),收缩之后的算法结果的值总和。利用的关系是:收缩之后的算法结果的值总和 ≥ 收缩之后的最优值总和。然后将没有收缩的与收缩的相联系,得到没有收缩情况下的关系。

A ≥ (1 - ε) OPT,可以任意接近OPT!
考试题型
M1. Show modelling ability, proof ability, and algorithm analysis ability (20’)
given an problem, try to model it formally.
proof the correctness of a simple algorithm.
give an analysis to a piece of Pseudo codes.
given a linear programming, figure out its duality, and find out the optimization solution. 【Required】

M2. Adopt algorithmic strategies to solve and analyze problems (greedy, D&C, DP, etc.) (30’)
- divide and conquer (Master Theorem)
- dynamic programming (design, border conditions, complexity) 【Required】
- greedy
- duality
- reduction
M3. Design algorithms and analysis on numbers, graphs, and flows. (25’)
- DFS, BFS
- Shortest path, MST
- Algorithms on DAG
- Algorithms on numbers (modular)
- Applications of network flows
M4. Prove a NPC problem (15’) 【Required: reduction】
- Prove an NP problem
- Prove an NPC problem
M5. Cope with NPH problem (10’)
- Approximation algorithm 【Required】
- Backtracking
- Local search